Military Theory VIII.

This is coolbert:

Frederick Lanchester.

Englishman who during World War One [WW1] [1916] devised mathematical equations to explain the nature of warfare.

Approached the problem as would an engineer, which he was [Lanchester was an engineer who had amazing success in his profession. Was instrumental in both the automotive and aeronautic industries in formulating many solutions to problems].

"Englishman Frederick W. Lanchester (1868-1946) was a major contributor to the foundation of automotive and aeronautical engineering. He also published works on radio, acoustics, warfare, and even relativity. His equations of combat form the basis of the science of operations research. (These equations have been used to formulate business strategy in recent times.) He was the first to describe the aeronautics of lift and drag. His automobile inventions include the gas engine starter, rack-and-pinion steering, disk brakes, four-wheel drive, and fuel injection."

Sought to model warfare creating differential equations that explain what is seen on the battlefield. Much as an engineer would model any other process or phenomenon.

Was successful.

Created a pair of differential equations THAT ARE USED TO THIS DAY IN COMPUTER SIMULATIONS OF WARFARE. Equations that have a degree of validity in modeling warfare on the battlefield

"Lanchester's equations. Basically, Lanchester observed that as ranged fires [indirect fires] replaced close combat as the primary casualty generator, the nature of warfare changed, and gave a great deal more emphasis on numeric superiority.

For example, in a battle between 1000 men on side A and 750 men on side B in the era of close combat (sword and shield), you'd wind up with 250 men on Side A and 0 on Side B after an engagement to the finish. That's a 75% loss rate for the superior force.

With ranged fire [indirect fire], you have a more complex situation."

"In his historic 1916 paper "Mathematics in Warfare," Lanchester presents two simple differential equations relating force attrition to the number of forces or weapons in opposition and to their effectiveness (see sidebar "Lanchester's Equations"). The equations' solutions show that the effectiveness of a force is directly proportional to the effectiveness of its weapons and to the square of its numbers. The following table illustrates how Lanchester's equations would apply in a classic artillery duel:

The Lanchester Exchange: Artillery Duel



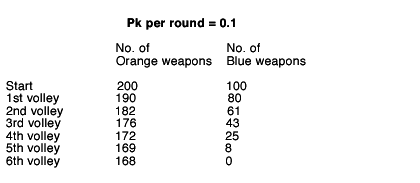
The table shows 200 weapons arrayed against 100 weapons with equal kill probabilities (Pk) of 10 percent. In the first round, Orange kills 20 Blues, and Blue kills 10 Oranges leaving 190 Oranges to kill 19 of the remaining 80 Blues, while the Blues kill 8 Oranges in the second round. At the end of the sixth round, all the Blues are gone and 168 Oranges (84 percent) remain.

Note that each side engages only the remaining live targets. If neither side can tell when it has killed a target, as in some artillery duels, both sides must continue to shoot at all the targets, thereby wasting part of their efforts. Lanchester analyzed this problem also and showed that the impact of numbers is a linear not square law."

[I would not be so rash to go into a more complicated explanation of these parallel differential modeling equations, other than to say that they exist and they have a degree of validity that has been vindicated.]

However, according to Du Puy, there is a problem with Lanchester's equations and how they apply to war in the REAL WORLD:

"Efforts to relate either or both of the Lanchester laws to historical attrition results have almost always failed"

"there will probably never be a close and easily recognizable relationship between real world attrition rates and those produced by his use of equations."

"his equations were valid only in situations in which the opposing forces are of equal quality, and are affected equally by the circumstances of the battle."

Such EQUAL QUALITY, AFFECTED EQUALLY is almost NOT found, if not at all found on the REAL battlefield.

Lanchester is "close", but not quite.

See more on Lanchester's equations by clicking here and here.

coolbert.